How is the Speculative Decoding Algorithm Constructed?

Speculative decoding accelerates the inference process of Large Language Models (LLMs) by using additional compute resources to reduce latency, while ensuring that the generation distribution remains consistent with the original model.

This article mainly shares the derivation ideas for the construction process of the Speculative Sampling algorithm mentioned in the paper “Fast Inference from Transformers via Speculative Decoding” ¹.

Engineering Foundation: Memory Wall

The main bottleneck in LLM inference is usually not compute capability (Compute), but memory bandwidth (Memory Bandwidth).

In autoregressive generation, for every token generated, the GPU needs to move massive model weights from memory (HBM) to the compute units. “Moving tens of GB of weights just to calculate one token” results in extremely low Arithmetic Intensity, severely wasting the GPU’s powerful parallel computing capabilities.

The core idea of Speculative Decoding is: use a small model (Draft Model) to quickly serially generate multiple draft tokens, and then let the large model (Target Model) verify these tokens in parallel. In this way, the large model can process multiple tokens with a single weight read, significantly improving arithmetic intensity and fully utilizing memory bandwidth.

Algorithm Process of Speculative Sampling

Here, Speculative sampling means a single step of speculative decoding that generates multiple tokens at once.

1. The small model serially samples $\gamma$ draft tokens ($x_1, \dots, x_\gamma$).
2. The large model calculates the true probability distribution $p(x)$ for these $\gamma$ positions in parallel.
3. Serial Verification: From $i=1$ to $\gamma$, calculate the acceptance probability $\alpha = \min(1, \frac{p(x_i)}{q(x_i)})$.
4. Truncation and Correction:
   • Once the $n$-th token is found to be rejected:
     • Discard $x_n$ and all subsequent drafts.
     • Sample a new token $t$ from the corrected distribution $p'(x) = \text{norm}(\max(0, p(x) - q(x)))$.
     • Return the first $n-1$ accepted tokens plus the new token $t$.
   • If all $\gamma$ tokens are accepted:
     • Sample an additional token $t \sim p(x_{\gamma+1} | \dots)$ and return all $\gamma+1$ tokens.

Construction Derivation

Speculative decoding is widely accepted because it mathematically guarantees losslessness: the final generated token distribution is completely consistent with the distribution generated by the large model token by token.

Given two distributions:

1. Draft Distribution $q(x)$: Generated by the small model, low cost to obtain.
2. Target Distribution $p(x)$: Generated by the large model, which is the distribution we truly want.

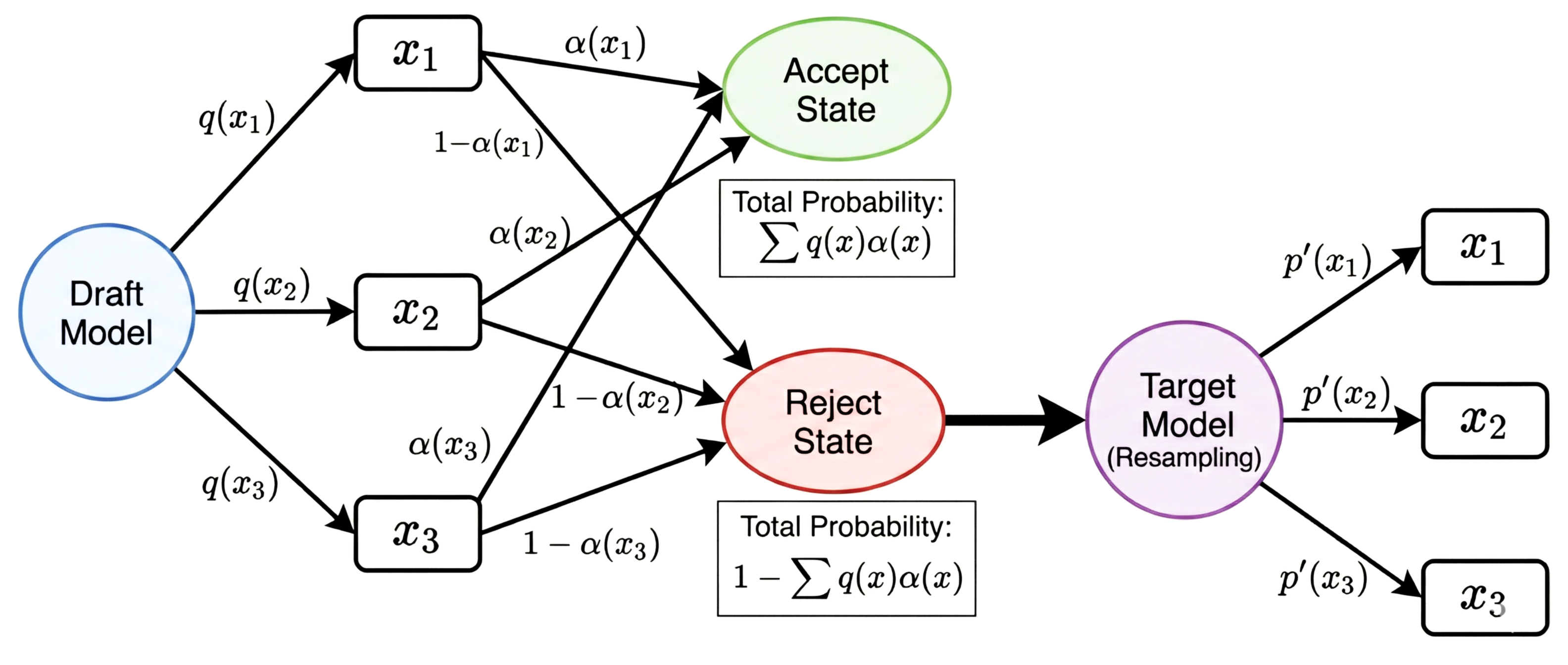
Our goal is to construct a sampling strategy such that the probability of the final output $x$ equals $p(x)$. This process can be decomposed into two parts: Accept and Resample.

$$ P(\text{output}=x) = \underbrace{q(x) \cdot \alpha(x)}_{\text{Accept}} + \underbrace{\beta \cdot p'(x)}_{\text{Resample}} = p(x) $$

Where $\alpha(x)$ is the acceptance probability, $\beta$ is the total rejection rate, and $p'(x)$ is the remedial distribution after rejection.

The first term represents the probability of selecting $x$ and accepting $x$, and the second term represents the probability of sampling $x$ from the corrected distribution when the first term is not realized (see the main figure of this article).

1. Constructing Acceptance Probability $\alpha(x)$

Construction constraints:

• To maximize the speedup ratio, we want to utilize draft tokens as much as possible: $\alpha(x)$ should be as close to 1 as possible.
• According to the Rejection Sampling principle, to ensure the probability after acceptance does not exceed the target probability $p(x)$: $\alpha(x) \leq \frac{p(x)}{q(x)}$.

Construction of acceptance strategy:

• When $q(x) \le p(x)$ (small model underestimates): 100% Accept.
• When $q(x) > p(x)$ (small model is overconfident): Accept with probability $\frac{p(x)}{q(x)}$ to eliminate excess probability mass.

So the acceptance probability is defined as:

$$ \alpha(x) = \min\left(1, \frac{p(x)}{q(x)}\right) $$

2. Calculating Total Rejection Rate $\beta$

$$ \begin{aligned} \beta &= 1 - P(\text{accept}) \\ &= 1 - \sum_x q(x)\alpha(x) \\ &= 1 - \sum_x q(x) \min\left(1, \frac{p(x)}{q(x)}\right) \\ &= 1 - \sum_x \min(q(x), p(x)) \\ &= \sum_x p(x) - \sum_x \min(q(x), p(x)) \\ &= \sum_x \max(0, p(x) - q(x)) \end{aligned} $$

3. Calculating Corrected Distribution $p'(x)$

When a draft token is rejected, we need to sample a token from a new distribution $p'(x)$ to replace it.

Intuitively, a part of the probability in $p(x)$ has already been filled by the accepted part of $q(x)$, which is $\min(q(x), p(x))$. The remaining “gap” is what we need to fill from $p'(x)$.

Derivation as follows:

$$ \begin{aligned} & \text{Accept}(x) + \text{Resample}(x) = p(x) \\ \iff & q(x) \cdot \min\left(1, \frac{p(x)}{q(x)}\right) + \beta \cdot p'(x) = p(x) \\ \iff & \min(q(x), p(x)) + \sum_x \max(0, p(x) - q(x)) \cdot p'(x) = p(x) \\ \iff & p'(x) = \frac{p(x) - \min(q(x), p(x))}{\sum_x \max(0, p(x) - q(x))} \\ \iff & p'(x) = \frac{\max(0, p(x) - q(x))}{\sum_x \max(0, p(x) - q(x))} \\ \iff & p'(x) = \text{norm}(\max(0, p(x) - q(x))) \end{aligned} $$

Therefore, the corrected sampling distribution $p'(x)$ is exactly the normalized $\max(0, p(x) - q(x))$.

Summary

Speculative sampling is essentially a process of “refund for overpayment and supplement for deficiency”:

1. Refund: Use $\min(1, p/q)$ to trim the probability that the small model “guessed too much”.
2. Supplement: Use $\max(0, p-q)$ to make up for the probability that the small model “missed”.

The combination of the two seamlessly restores the target distribution $p(x)$.

Citation

@article{shichaosong2025howisthespecula,
  title = {How is the Speculative Decoding Algorithm Constructed?},
  author = {Shichao Song},
  journal = {The Kiseki Log},
  year = {2025},
  month = {December},
  url = {https://ki-seki.github.io/posts/251226-spec-decoding/}
}

References